>_

Tag: Gradient descent

Neural Networs: the fundamental component of modern AI
Neural networks are at the core of modern artificial intelligence, powering everything from image recognition and natural language processing to medical diagnostics and self-driving cars. While they may seem complex due to their mathematical foundations, they rely on fundamental calculus concepts that even someone with a high school diploma can understand.

This post explores how neural networks work and how they are trained to recognize patterns in data like text and images—all without using overly technical or confusing lingo.

Neurons

An artificial neuron is the elementary component of a neural network. Neurons receive 1 or more inputs and plug them into a function to produce an output. This function calculates a weighted sum of the inputs and adds a bias term. It does so by multiplying the inputs by their corresponding weight and then adding the bias term.

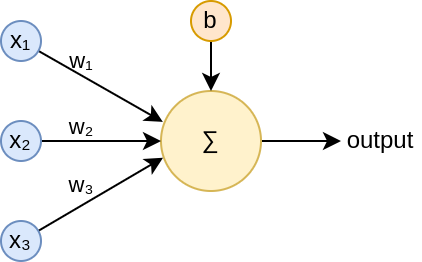
For a neuron with 3 inputs, such as the one in the image, the neuron calculates: $\hat y = x_1 w_1 + x_2 w_2 + x_3 w_3 + b$ . Where $\hat y$ is the prediction or output. Very simple.

how do we set the value of our weights and bias (parameters)?

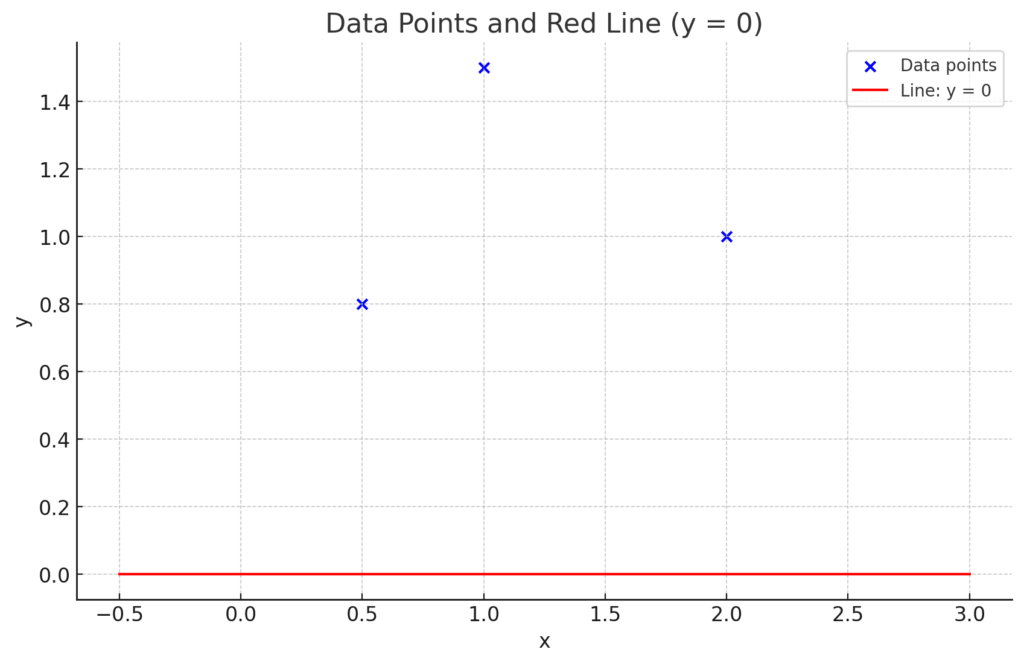
Imagine we want to use our neural network to predict the grade (target) for a course by giving it the hours we studied (input), and we have the following data:

Hours Studied (input) Grade (target)
2 3
4 5
6 4
8 6
10 8

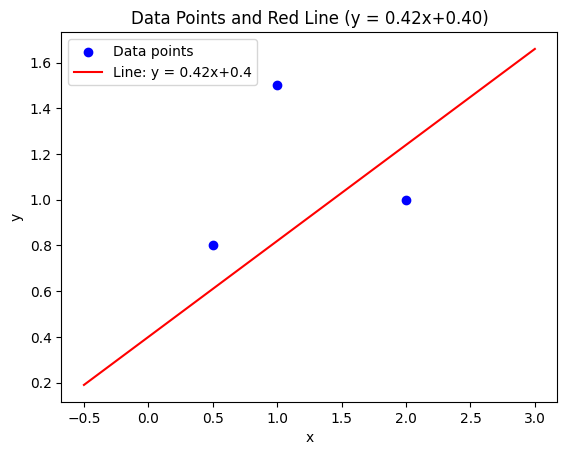
For this scenario, we have one input variable and one target variable. Our neuron’s calculation follows the equation:

$\hat y = x_1 w_1 + b$

If this equation looks familiar, that’s because it represents the equation of a line. Our goal is to find the best values for $w$ (slope) and $b$ (intercept) that allow the model to fit our data optimally.

To evaluate how well the model fits, we calculate the Mean Squared Error (MSE)—the average squared distance between each data point and the predicted values from our model. The reason we square the distances is to ensure that negative and positive errors don’t cancel each other out.

To find the best-fitting model, we start with random values for $w$ and $b$ , then adjust them to minimize the MSE. The values that result in the lowest MSE define the optimal model for our dataset.

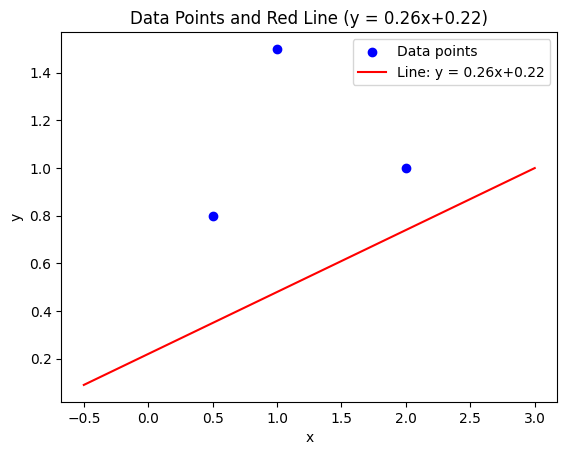
Try yourself to find the values that minimize the MSE:

Adjust parameters to Fit Points

Weight (slope): 1

Bias (intercept): 1

Equation: y = 1.00x + 1.00

MSE: 0

For learning purposes, we used a trial-and-error approach to estimate the best values for www and bbb. However, in real neural networks, these parameters are optimized using gradient descent

The most optimum values for this example are $w=0.55x$ and $b=1.90$ .

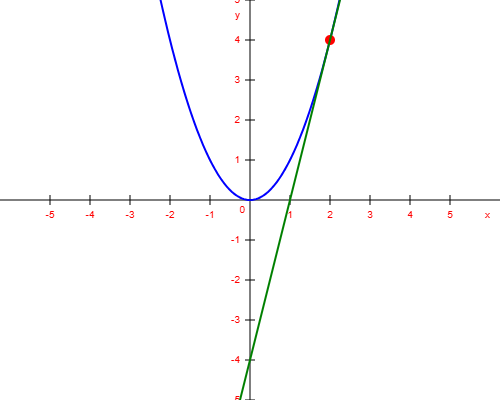
Onece model has been optimized, we can use it to predict outcomes for unknown data by plugging the input into our equation. For example, we want to predict our grade if we studied for 7 hours, but we don’t have specific data for this case. Although we don’t have this exact data point in our dataset, our model can generalize based on the learned relationships and give us an approximate grade value.

$\hat y = wx+b$

$= 0.55x + 1.9$

$= 0.55(7)+1.9 = 5.75$

New Graph of the Line, Evaluated Point, and Given Points

According to our model, if we study 7 hours, we are expected to get a grade of 5.75.

Note. This example has only one input, but the process is the same if you have more than one input.

Neural Networks

Now that we know how a neuron works, we can stack them in layers, connecting all neurons in one layer to all the neurons in the previous layer. This kind of neural network is called a fully connected neural networks, and they look like this:

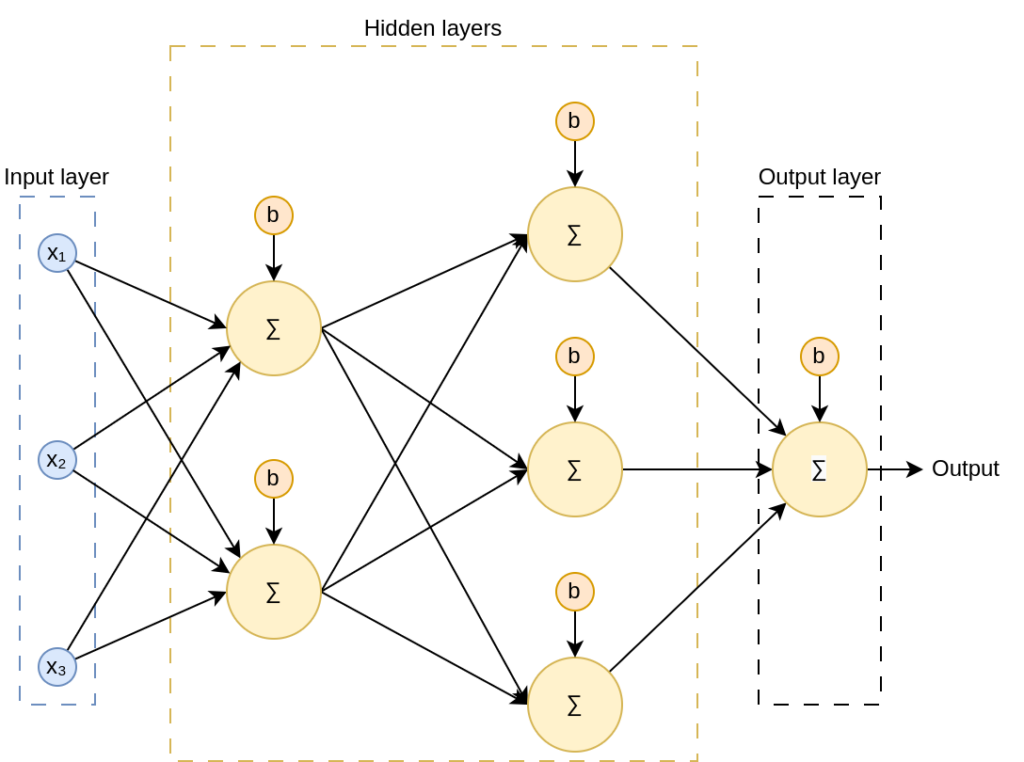
Observe how, for the hidden neurons (those in the hidden layers), the outputs from the preceding layers serve as inputs. Also, note that although weights are not represented in the image, all connections have their own weight.

By stacking neurons, the network can model not just linearly shaped data but also data with complex patterns and structures. Think of each neuron as a line, and by stacking multiple lines, you can build a model that can make generalizations (predictions) from your data.

Activation function

So far, we have sum a bunch of lines, but there is a problem with that; The sum of two or more lines is a line. So, a neural network like the one in the image above would give us a single line as an output. Therefore, it wouldn’t be any better than a single neuron.

We must apply some nonlinearity to each neuron to prevent neural networks from collapsing into a single neuron. This nonlinearity we use is called activation function, and are denoted as $\sigma (z)$ . Where $z = w_ix_i + b_i$ .

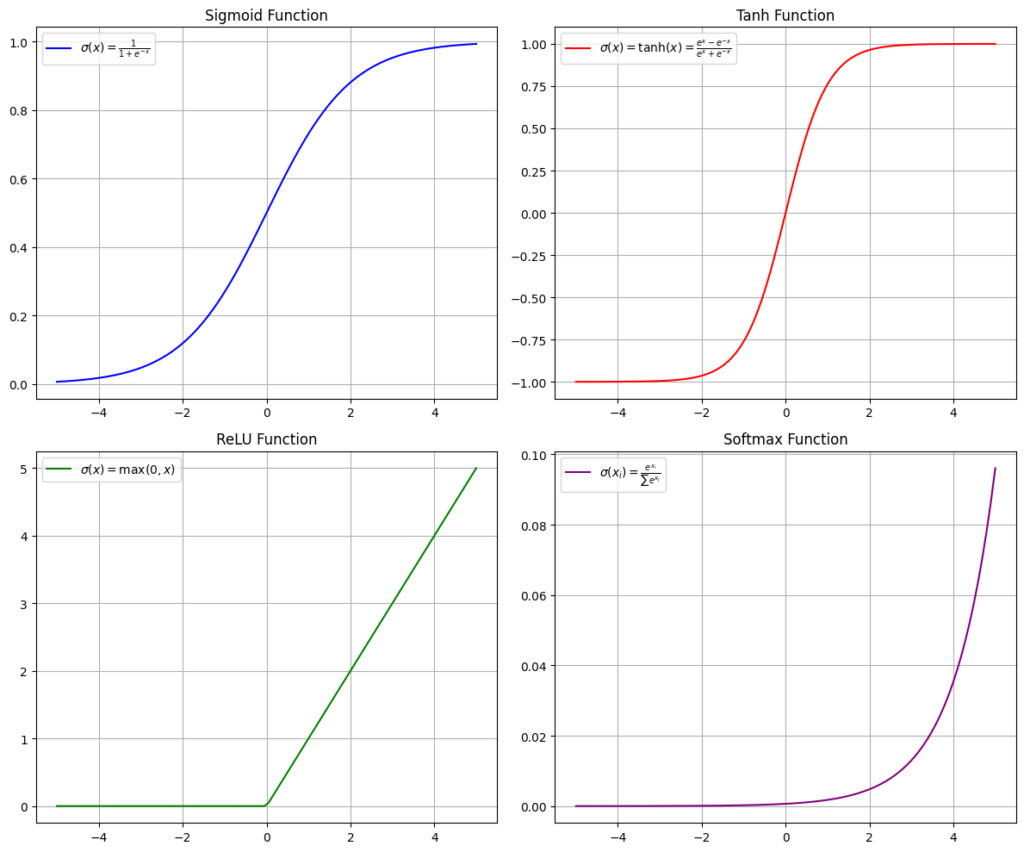
Some of the most known activation functions are:
- Softmax
  - $\sigma(z_i)=\frac{e^x_i}{\sum{e^x_j}}$
- Sigmoid
  - $\sigma(z)=\frac{1}{1+e^{-z}}$
- RELU
  - $\sigma(z)=max(0, x)$
- Tanh
  - $\sigma(z)=tanh(z)=\frac{e^x - e^{-x}}{e^x + e^{-x}}$
Don’t worry if you don’t understand these equations; just focus on the fact that these activation functions add nonlinearity, and they look like this:

We applied an activation function to the outputs of each neuron, enabling us to process these outputs without collapsing and to fit data that was non-linearly shaped or followed complex patterns. The prediction for the neuron

The resulting diagram of a neuron including the activation function would be:

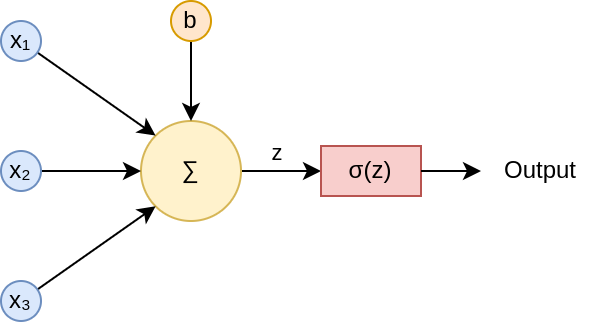
Backpropagation

When we run the calculations through our neural network for the first time, we’ll get a random output since all the weights and biases (parameters) are initialized randomly.

To optimize these parameters, we need to calculate the error for the obtained output and then propagate that error backward through all the previous layers.

Then, we use the gradient descent to optimize the parameters across the network. Neurons that contribute the most to the error will be penalized, and their impact will be reduced by adjusting their weights. On the other hand, neurons that contribute more to the desired output will gain more importance, as their weights are adjusted to improve the overall network performance.

If you’re interested in learning how backpropagation works and the math behind it, you can read my post about backpropagation.

Now what?

To sum up, training a neural network involves iterating through numerous steps of forward and backward passes and adjusting the weights and biases at each layer to minimize the error. This is achieved through techniques like gradient descent and backpropagation, which penalize neurons responsible for the most significant errors. At the same time, those that contribute positively to the output are strengthened. Over time, this process allows the network to learn from the data and make increasingly accurate predictions.

Now that we understand how neural networks work and how backpropagation and gradient descent are used to optimize their parameters, we can apply these networks to process a wide range of data. For instance, in image processing, each pixel can serve as an input to the network, while in Natural Language Processing (NLP), words or even characters can be the inputs. This versatility allows neural networks to solve complex problems across various domains, making them invaluable in fields like computer vision, NLP, and beyond.
March 18, 2025
Understanding Neural Networks: A Deep Dive into Backpropagation

Backpropagation is a crucial algorithm used in neural network training. It involves calculating the error at the output layer and then propagating that error backward through the network to adjust the weights of the neurons in each layer. Afterward, an optimization algorithm, typically gradient descent, uses this error to update the parameters (weights and biases) of the network, enabling the model to learn and improve its performance.

How Backpropagation Works

The Mathematics Behind Backpropagation

March 19, 2025
Optimization: Gradient Descent
Gradient descent is one of the most used algorithms to optimize a function. Optimizing a function means finding the hyperparameter values for that function that give us the best possible outcome.

Gradient descent has broad applications, but in this text, we will focus on its use in Machine Learning to minimize model loss in a linear function.

Cost function

Before optimizing anything, we first need a way to measure performance. This is where the loss function comes in. In simple terms, the loss function tells us how far off our model’s predictions are from the actual values. It’s a crucial guide for improving our model.

Some of the most commonly used loss functions include Mean Squared Error (MSE) for regression tasks and cross-entropy for classification problems.

Mean Squared Error

The Mean Squared Error (MSE) is the average of the squared differences between the observed (actual) values and the values predicted by the model. By squaring the differences, we ensure that negative errors don’t cancel out positive ones. You might wonder why we don’t simply take the absolute differences instead. The reason is that squaring the errors penalizes larger mistakes more heavily than smaller ones, which can be useful in emphasizing and correcting significant prediction errors. Mean Squared error is represented by the follwing equation:

$\text{MSE} =\frac{1}{n} \sum_{i=1}^{n}(y - \hat y)^2$

Where $\hat y$ is the predicted value and $y$ is the observed value./

Illustrative example

Imagine we have a linear model, represented by a red line, and we want to fit it to a set of data points, shown as black dots. Try to find the best hyperparameters—specifically the slope and the bias—that minimize the model’s error. This error is measured using Mean Squared Error (MSE), which we can visualize as blue squares representing the squared distances between the predicted values on the red line and the actual data points. The smaller these blue squares, the better our model fits the data.

Weight (slope): 1

Bias (intercept): 1

Equation: y = 1.00x + 1.00

MSE: 0

What is the gradient?

Let’s say we want to optimize a loss function defined by the equation $y=x^2$ , where $y$ represents the loss value and xxx is the hyperparameter we want to optimize. If we set $x=2$ , the loss becomes $y=4$

While it’s easy to see that the optimal value of $x$ is 0—since we know the shape of the function—in real-world scenarios, the loss function is often much more complex and not visually obvious. So, how can we figure out whether to increase or decrease $x$ to reduce the loss?

Spoiler alert: we can do this by calculating the gradient.

By taking the derivative of the loss function with respect to $x$ , we obtain the gradient at that point. For $x=2$ , the derivative of $y = x^2$ is $y'=2x$ , so the gradient is $2 \times 2=4$ . This gradient represents the slope of the tangent line at that point.

To minimize the loss, we want to move in the direction that reduces the loss the fastest—that is, in the opposite direction of the gradient. Our goal is to reach a point where the gradient is 0 (or very close to it), which indicates that we’ve found a minimum in the loss function.

Learning rate

However, there are situations where we might start far from the optimal value of our parameter. In such cases, the gradient tends to be steeper—the farther we are from the minimum, the larger the gradient usually is. This suggests that we might want to take larger steps when the gradient is large, and smaller steps when the gradient is small.

This is where the learning rate comes into play. The learning rate is a small positive value that controls how much of the gradient we actually use to update our parameter. Instead of subtracting the full gradient from our parameter, we subtract only a fraction of it. This helps us move in the direction of lower loss without overshooting the minimum.

Gradien descent step by step

For the following dataset lets build a linear model to make some predictions:

$((x_1, y_1) = (0.5, 0.8))$

$((x_2, y_2) = (2.0, 1.0)$

$((x_3, y_3) = (1.0, 1.5))$

In a linear regression model, we have two parameters: the slope and the intercept. Therefore, we need to calculate the gradient for both of them.

$f(x) = mx + b$

Where:
- $m$ is the slope,
- $b$ is the intercept
Before starting we assking any value both variables to have something to improve on.

Step 1: Initialize paremeters

Before starting the optimization process, we assign an initial value to both variables so we have something to improve upon.
- $m=0$
- $b=0$
Step 2: Calculate Loss

We’ll use Mean Squared Error (MSE):

$\text{Loss}=\frac{1}{n} \sum_{i=1}^{n} (y_i - f(x_i))^2 =\frac{1}{n} \sum_{i=1}^{n} (y_i -(mx_i + b))^2$

Predictions with $m=0, b=0$

$f(x_i)=0$ for all x values.

Step 3: Compute gradients

We calculate the partial derivatives of the loss with respect to $m$ and $b$ :

Gradient with respect to $m$ :

$\frac{\partial \text{Loss}}{\partial m} = -\frac{2}{n} \sum_{i=1}^{n} x_i \left( y_i - (m x_i + b) \right)$

$\frac{\partial \text{Loss}}{\partial m} = -\frac{2}{3} \left[ 0.5 \cdot (0.8 - 0) + 2 \cdot (1 - 0) + 1 \cdot (1.5 - 0) \right] = -\frac{2}{3} (3.9) = -2.6$

Gradient with respect to $b$ :

$\frac{\partial \text{Loss }}{\partial b} = -\frac{2}{n} \sum_{i=1}^{n} \left( y_i - (m x_i + b) \right)$

$\frac{\partial \text{Loss}}{\partial m} = -\frac{2}{3} \left[ (0.8 - 0) + (1 - 0) + (1.5 - 0) \right] = -\frac{2}{3} (3.3) = -2.2$

Step 4: Update parameters

Using a learning rate $\alpha = 0.1$ , we update $m$ :

$m_{\text{new}} = m_{\text{old}} - \alpha \cdot \frac{\partial \text{Loss}}{\partial m}$

$m_{\text{new}} = 0 - 0.1 \cdot (-2.6) = 0.26$

Next, we update $b$

$m_{\text{new}} = m_{\text{old}} - \alpha \cdot \frac{\partial \text{Loss}}{\partial b}$

$m_{\text{new}} = 0 - 0.1 \cdot (-2.6) = 0.22$

Note: We subtract the gradient from the current value because we want to move in the opposite direction of the gradient, as explained earlier.

Now, we plug these updated values for mmm and bbb into our linear function:

$f(x) = 0.26x + 0.22$

And we plot the updated model:

The model has significantly improved compared to the initial version.

After continuing the iterations for 3 more steps, we arrive at the following values:

$m=0.42$

$b=0.40$

These values yield the following model:

Note: The learning rate α=0.1\alpha = 0.1α=0.1 is not an ideal value. Typically, smaller learning rates are used, as larger values may cause the model to have trouble converging.
January 23, 2025