Why you should never use MSE as a loss function for NN classification problems

The MNIST dataset is an extensive database of handwritten digits commonly used to train NN for image processing systems. Each example in the dataset is a 28×28 image normalized in a matrix with the grayscale values for each pixel. The goal for this dataset is to correctly classify the handwritten digits.

To process the data in the MNIST dataset, we need a neural network with at least 28×28=784 input nodes and 10 output nodes (one for each digit). The idea is to get a probability distribution for all the digits, and the digit with the highest probability will be our prediction.

For MSE loss is given by the following equation:

   

In the proposed MNIST problem, the model’s accuracy depends on the probability of predicting the correct label. However, this loss function measures the arithmetic difference between labels, which is not meaningful. Imagine the following scenario:

Each circle represents an output node, one for each digit, and the probability for a single example fed to the network. In this scenario, the predicted value would be 2 since it has the most significant probability, but let’s imagine that the observed (correct) value is 9.

If we use the squared error to measure the loss:

   

This would tell our model that it did a terrible job predicting the label. However, if we see the probabilities in the previous image, we will notice that the second highest probability was 9. Therefore, our model is not so far from the correct output.

What if we use a different loss function?

Now that we know MSE is not a good loss function for this problem, what if we try with a probability-based loss function:

Let’s use the following function:

   

Although it is probability-based, this loss function does not make much sense. The loss is the same as the probability of the correct output, and since we want to reduce the loss, we would reduce the likelihood of obtaining the correct output. For the same scenario that before:

   

This L = 0.2 is the loss we want to minimize, but if we do so, we would also reduce P(9). Which is the probability of the correct output.

What is a good loss function?

A standard loss function for classification problems is the cross-entropy loss function:

   

Where P(y) is the probability of getting the correct output. The plot for this function is the following:

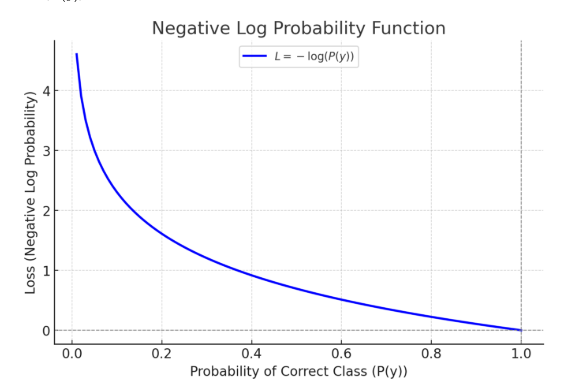
This is a good function for the proposed problem since it will strongly penalize low values of P(y) (probability of getting the correct output) and penalize a little for high P(y) values.
For the proposed problem, we have:

   

But if we get a higher value for P(9), such as 0.95:

   

Our model gets a much lower loss and a lower penalization. This makes much more sense than the other functions since this one penalizes a few confident and accurate predictions.